Trong trận chiến giữa A và B, vùng chiến đấu được chia thành một lưới các ô vuông gồm m dòng, n cột. Trên lưới có một số ô đã có chướng ngại vật dựng sẵn (ô màu đen) nên A không thể đi qua được mà phải đi vòng thông qua các ô trống (ô màu trắng): A muốn di chuyển từ ô ~(1, 1)~ đến ô ~(m, n)~ để tiến đánh B. Vì vậy, B đã tìm cách bố trí thêm chướng ngại vật ở một số ô trống để nhằm mục đích ngăn cản A không thể thực hiện được ý định của mình. Xuất phát từ ô ~(1, 1)~, A chỉ có thể di chuyển sang các ô trống có chung cạnh. B chỉ được bố trí thêm chướng ngại vật ở các ô trên các dòng từ 2 đến m-1.

Yêu cầu:

Hãy tìm số lượng ít nhất các ô mà B phải bố trí thêm chướng ngại vật để A không thể di chuyển từ ô ~(1, 1)~ đến ô ~(m, n)~.

Dữ liệu vào:

Cho trong tệp văn bản MILITARY.INP có cấu trúc như sau:

• Dòng đầu gồm hai số nguyên dương m và n cách nhau 1 ký tự trắng ~(1 \leq m, n \leq 1000)~.
• m dòng tiếp theo, mỗi dòng ghi một xâu gồm n ký tự . (ô màu trắng) hoặc # (ô màu đen). Chú ý rằng dòng đầu và dòng cuối không có ô màu đen.

Dữ liệu ra:

Ghi ra tệp văn bản MILITARY.OUT một số nguyên duy nhất là số lượng ít nhất các ô mà B cần phải bố trí thêm chướng ngại vật.

Ví dụ:

Input:MILITARY.INP

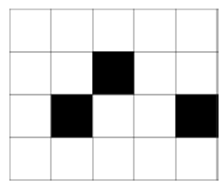
4 5
.....
..#..
.#..#
.....

Output:MILITARY.OUT

2

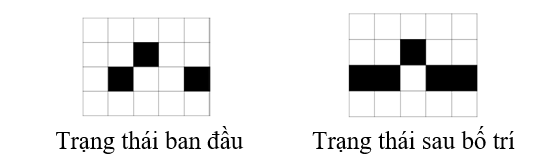
Giải thích: B chỉ cần bố trí thêm chướng ngại vật ở các ô ~(3,1)~ và ô ~(3,4)~.