Giáo sư X đang nghiên cứu về hệ sinh thái trên hai hành tinh Alpha và Beta. Nghiên cứu cần phải thực hiện ~n~ thí nghiệm, các thí nghiệm được đánh số từ 1 tới ~n~. Mỗi thí nghiệm được gán nhãn bằng một kí tự chữ cái thuộc ~{A, B, C}~:

• A: Thí nghiệm chỉ có thể thực hiện trên hành tinh Alpha.
• B: Thí nghiệm chỉ có thể thực hiện trên hành tinh Beta.
• C: Thí nghiệm có thể thực hiện trên hành tinh Alpha hoặc Beta đều được.

Ngoài ra, quy trình thí nghiệm cần phải thỏa mãn ~m~ ràng buộc. Ràng buộc thứ ~i~ được cho bởi cặp số nguyên ~(x_i, y_i)~ với ý nghĩa: Thí nghiệm ~y_i~ chỉ có thể thực hiện được khi thí nghiệm ~x_i~ đã thực hiện xong.

Yêu cầu: Vì việc đi lại giữa hai hành tinh rất tốn kém và mất nhiều thời gian, hãy lập một kế hoạch thực hiện các thí nghiệm cho giáo sư X để số lần di chuyển giữa hai hành tinh Alpha và Beta là ít nhất. Cho biết ban đầu giáo sư X đang ở hành tinh Alpha.

Dữ liệu vào:

Cho trong file văn bản SUPERPRO.INP, có cấu trúc như sau:

• Dòng 1: Ghi hai số nguyên dương ~n, m~ ~(1 \leq n, m \leq 10^5)~, hai số được ghi cách nhau ít nhất một dấu cách.
• Dòng 2: Ghi ~n~ kí tự chữ cái thuộc ~{A, B, C}~ liền nhau, kí tự thứ ~k~ là nhãn của thí nghiệm ~k~.
• Dòng thứ ~i~ trong ~m~ dòng tiếp theo: Mỗi dòng ghi hai số nguyên ~x_i, y_i~ tương ứng với ràng buộc thứ ~i~ trong ~m~ ràng buộc ~(1 \leq i \leq m)~, hai số được ghi cách nhau ít nhất một dấu cách.

Kết quả:

Ghi ra file văn bản SUPERPRO.OUT, theo cấu trúc như sau:

• Dòng 1: Ghi số nguyên ~d~, là số lần di chuyển giữa hai hành tinh Alpha và Beta. Nếu bài toán không có nghiệm thì in ra -1.

Ví dụ:

Input: SUPERPRO.INP

11 12
AABAABABBBC
1  2
2  3
2  10
3  4
3  11
7  11
8  7
9  10
10  3
10  11
11  5
11 6

Output: SUPERPRO.OUT

3

Giải thích

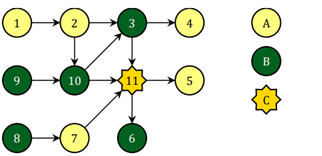
Một trong các phương án là: - Làm thí nghiệm 1 và 2 trên Alpha. - Làm thí nghiệm 8, 9, 10 và 3 trên Beta. - Làm thí nghiệm 7, 11, 5, 4 trên Alpha. - Làm thí nghiệm 6 trên Beta. Vậy có 3 lần di chuyển: Alpha ~\to~ Beta ~\to~ Alpha ~\to~ Beta.